https://kimjy99.github.io/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0/ddpm/
[논문리뷰] Denoising Diffusion Probabilistic Models (DDPM)
DDPM 논문 리뷰 (NeurIPS 2020)
kimjy99.github.io
[개념 정리] Diffusion Model 과 DDPM 수식 유도 과정
이전글 에서 Diffusion Model과 DDPM(Denosing Diffusion Probabilistic Model)의 개념에 대해서 알아봤습니다. 이번 글에서는 수식 유도 과정을 다뤄보겠습니다.이전글에서 Diffusion모델은 Noise를 주입을 위해 사
xoft.tistory.com
https://jang-inspiration.com/ddpm-2
Diffusion Process란, 시간에 따라 확률 분포가 점진적으로 변화(확산)하는 과정을 이야기한다. Deep Unsupervised Learning using Nonequilibrium Thermodynamics(ICML 2015) 논문에서, 저자는 Diffusion Process를 사용하는데, 가우시안 같은 분포 → 데이터(target) 분포로 점진적으로 변화하는 Generative Marcov Chain을 사용한다.
Markov chain 이란?
직역으로 본다면, Markov 성질을 가진 Dicrete-time Conditional Sequence 라고 볼 수 있다. 여기서 Markov 성질은 '특정 상태의 확률은 오직 과거의 상태에 의존한다'라는 것이다.
여러 상태 (x1, x2, · · ·, xt)가 있고, xi → xj로 이동할 조건부 확률분포(Conditional distribution) T(xj | xi)가 주어져 있다. 매턴(t)마다 이 확률 값에 따라 상태들 사이를 이동하는 것을 말한다. Markov chain은 어떤 지점에서 출발하더라도 상태 사이를 충분히 많은 횟수만큼 이동하게 되면 각 상태의 방문횟수 비율은 일정한 값으로 수렴(즉, 특정 확률 분포로 수렴)하게 된다.



상태 전이도(state transition diagram)이 위와 같은 그림으로 나타낸다면, 전이확률 행렬로 표현할 수 있다.

여기서 특정일 날씨 중 80% '맑음'이였다면, 특정일 기준 모레가 '맑음 확률'은 = 0.8 x 0.565 + 0.2 x 0.362 = 0.524가 된다.
이러한 상태에서 충분히 많은 횟수를 반복하게 된다면, '전이확률행렬이 변하지 않는 상태'가 오는데, 이를 두고 steady state라고 부르고, 확률이 직전 상태와 동일하게 수렴하게 된다. 즉, 특정일이 t라고 정의할 때 t-1에서 확률이 P(t) = P(t-1)로 동일하게 된다는 것이다. 이러한 확률 분포를 정적분포(Stationary/Invariant probability)이라고 부르게 된다.


여기서 중요한 점이 있는데, 미래가 과거와는 독립이고 오로지 직전 시점(t-1)에만 영향을 받는다는 것이다.
Deep Unsupervised Learning using Nonequilibrium Thermodynamics(ICML 2015)
1. Algorithm
목표
1) foward diffusion process를 통해 복잡한 데이터 분포를 쉽고 tractable한 분포로 전환한다. q(x1, x2, · · ·, xt)
2) 유한한 시간 동안의 reversal diffusion process를 통해 새로운 생성 모델 분포를 정의한다. p(x1, x2, · · ·, xt)
1.1 Foward Trajectory

실제 데이터 분포 label q(x)를 tractable하게 잘 정의된 분포 π(y)로 만드는 것이다.
(1)항은 tractable 잘 정의된 분포를 정의한 것인데 수식 자체가 의미하는 것은 Invariant probability를 정의한 것이다. 여기서 아까 이야기했듯이, Markov Chain은 전이행렬을 통해서 상태 이동이 수행된다. 일종의 전이행렬 kernel을 정의하게 되는데 그것이 (2)항이다. β는 diffusion rate로 매개변수를 의미한다.

1.2 Reverse Trajectory

tractable하게 잘 정의된 분포 π(y), Invariant Probability를 Markov Chain 속성을 사용해서 새로운 생성 모델의 distributions를 만들어내는 것이다.
연속적인 확산을 위해서 reverse가 forawrd와 같은 함수 형태로 되어야 한다고 한다. 논문의 실험에서 해당 함수들은 모두 MLP이다.
1.3 Model Probabilty
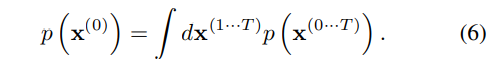
Reversal Diffusion Process를 통해서 나온 데이터 분포들 p(x0, · · ·, xT)에 대해서 p(x0) 분포만 남기기 위해서 Marginalization 수식을 통해서 계산한 것이다. 하지만 (6)항은 계산이 불가능(Intracable)하기 때문에 annealed importance sampling과 Jarzynski equality로부터 상대적 확률을 구하게 된다.

1.4 Training
학습은 Model의 Log likelihood를 최대화하는 방향으로 진행한다.



1.5 Multiplying Distributions, and Computing Posteriors
모델의 분포 p(x0)과 다른 분포 r(x0)을 곱하여 새로운 분포 ~p(x0)을 만드는 것이다.





Denoising Diffusion Probabilistic Models(NIPS 2020)

Reversal signal이 파괴될 때까지 sampling의 반대 방향으로 noise를 점진적으로 추가하는 Markov chain을 진행하고 그 역을 통해 데이터를 샘플링하는 것이다. 소량의 Gaussian noise를 넣는 것만으로 간단한 NN parameterization이 가능하다.
Diffusion Model의 궁극적인 목표는 Reverse process를 통해서 만들어지는 p(x0)을 찾는 것이다. 저자는 당시 높은 퀄리티의 샘플을 Diffusion Model을 통해서 입증이 되어있지 않았기에 해당 논문을 통해서 증명하려고 한다.
이 논문의 모델은 다른 확률 기반 생성 모델보다 낮은 log-likelihood를 가진다. 즉, 분포를 얼마나 '잘' 모델링하고 있는지를 보여주는 수치가 낮게 측정된다고 한다. 다만, Annealed Importance Sampling 방식으로 추정한 에너지 기반 모델들보다는 높은 log-likelihood를 가진다.
1. Background

이미지에서 xT에서 reverse markov process를 거쳐서 p(x0:T)를 복원하는 수식이다. 여기서 reverse process에 대해서 가우시안 분포로써 정의했는데, 직역하면 xt 분포가 주어졌을 때 xt-1 분포를 샘플링(역방향)한다는 것이다.


여기서 알아야하는 것은 일반적으로 Markov 체인을 정의할 때 한 단계 전 상태만으로 다음상태가 결정된다는 것이다. 그렇기 때문에 조건부 독립이므로, 각각 곱셈을 통하게 되면 x0이 주어졌을때 x0 → xT으로 점진적으로 바꾸는 Markov Chain을 정의할 수 있는 것이다. DDPM 논문에서는 forward markov process 과정에서 노이즈를 추가해야하는데, βt만큼의 노이즈(분산)를 추가하는 것이다. 그리고 Markov 성질인 이전상태에만 의존한다는 조건도 충족한다.

주목할만 점은 x0 → xt로 한꺼번에 바꾸는 foward markov process를 정의할 수 있다. αt = 1 - βt로 치환한 것이다. 그리고 노이즈를 누적시키는 방법은 단순하게 α1 x α2 x · · · x αt를 통해서 누적할 수 있다.
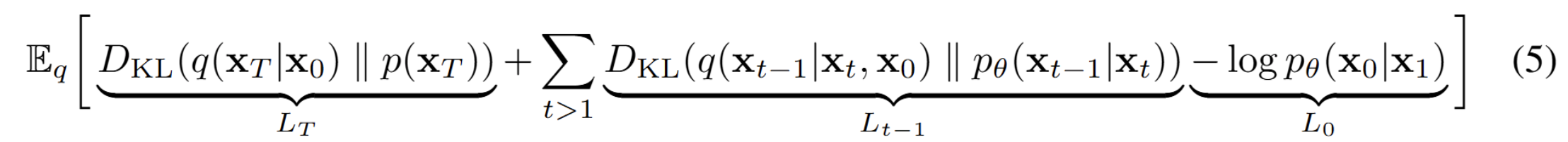
(1) L_T
Foward Diffuision(markov) process에서 x0 → xT까지 '노이즈를 점진적으로 섞은' 분포가 (4)항에서 볼 수 있듯이 q(xT | x0)이다. 분포 p(xT)와 q(xT | x0)이 얼마나 다른지를 KL divergence로 판단하는 것이다. Figure2. 를 보면 직관적으로 이해할 수 있다. 원본 이미지 → 노이즈를 섞은 이미지로 변환(q(xT | x0))과 original noise 분포 p(xT)와의 KL Divergence를 통해서 두 분포 간의 '유사하지 않음'을 측정하는 것이다.
L_T는 p(xT)라는 노이즈 분포를 원하는 노이즈 분포로 만들기 위한 핵심적인 항이다. 다만, 논문의 실험에서는 forward markov process에서 중요한 역할을 수행하는 βt를 상수로 두고 있기 때문에 L_T항은 무시(학습되지 않기 때문)하여도 된다고 소개한다.
(2) L_t-1
Reverse markov process에서 핵심적인 항입니다. q(xt-1 | xt, x0)은 Forawd로 x0 → xt를 만든 실제 확률을 역으로 추론한 형태이다. 즉, Foward markov process에다가 Bayes 정리를 통해서 유도한 식이다. q(xt | xt-1)은 학습을 통해서 완성되는 것이 아니고 데이터 x0에서 노이즈 xT로 가는 과정을 인위적으로 정의한 것이다. p(xt-1 | xt)는 모델이 학습해야하는 reverse markov kernel이다. 결과적으로, KL Divergence의 값을 작게 만듦으로써 노이즈에서 점진적으로 x0을 복원하는 과정이 진짜 데이터 분포(Posterior)와 가까워져, 좋은 생성 품질을 얻게 되는 것이다.
증명
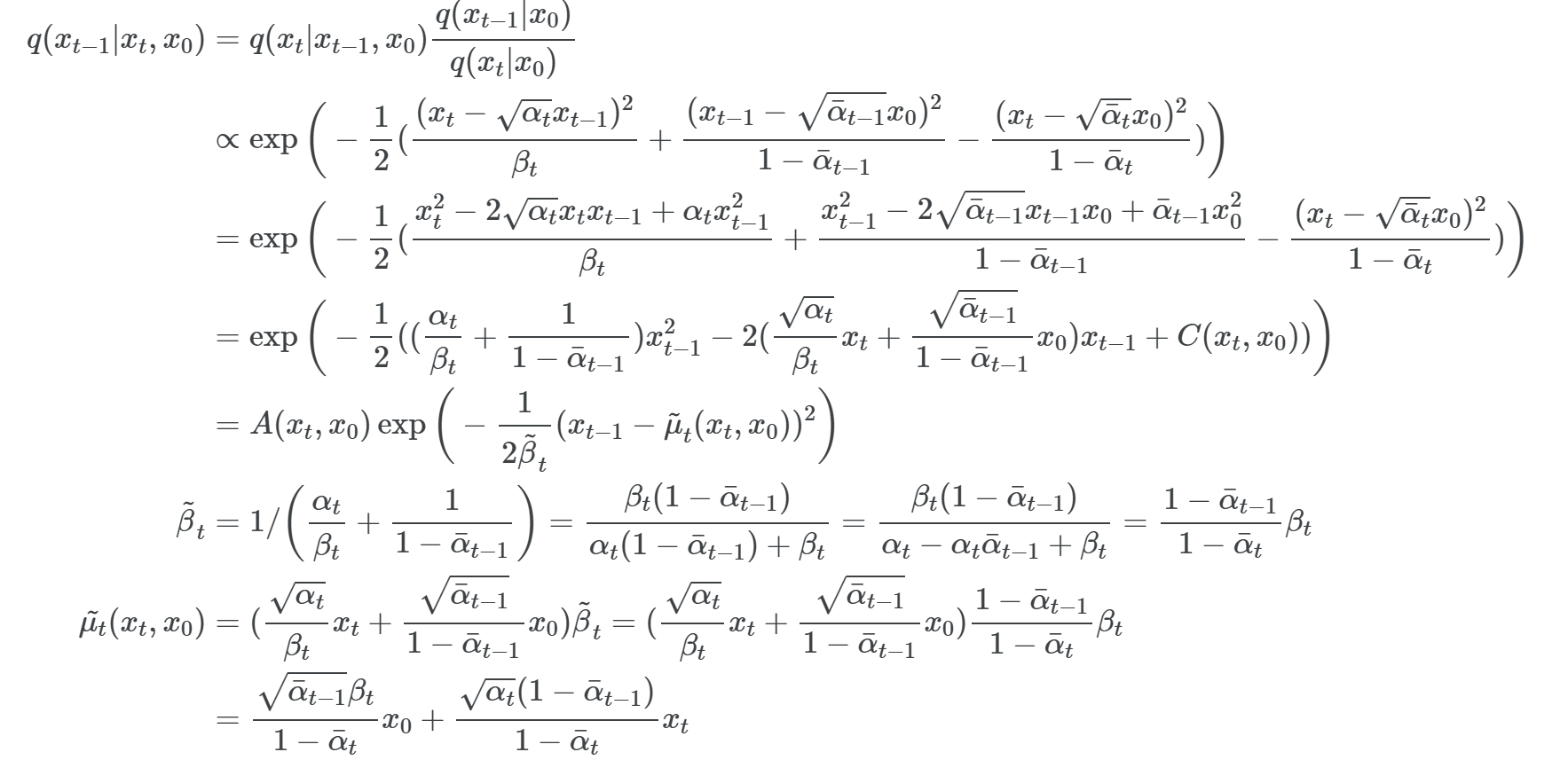
그러면, 어떻게 Reverse markov process를 구성하는 값들을 구성해야 하는지 살펴보자.


증명


우리는 (4)항을 통해서 xt(x0, ϵ)라는 중간 시점 t의 xt를 closed-form 식으로 나타낼 수 있다는 것을 확인하였다. Lt-1의 식을 foward markov 분포의 posterior를 통해 식을 풀어볼 수 있다고 한다.


(9), (10)항이 보여주고자 하는 것은 Foward 노이즈 xt(x0, ϵ)를 통해서 μθ의 input으로 줄 수 있다는 것이고 μθ는 논문의 말처럼 위와 같은 구조를 보이고 있습니다. 지금까지 μθ를 어떻게 정의(parameterization)하는지에 대한 고민에 대한 답에 대해서, 저잗르은 ϵ을 학습하고 예측함으로써 μθ를 구성할 수 있다는 것을 보여준다.

μθ는 결국 ~μθ와 닮아가야 한다. 그리고 "ϵ 예측" 방식을 선택하게 되면 (11)항과 같은 형태가 된다. (ϵθ 함수는 xt로부터 noise ϵ를 예측하는 함수이다.)


논문에서 나오는 수도코드이다. Training이 의미하는 것은 x0 → xT로 만드는 노이즈 ϵθ에 대해서 학습하게 되는 것이다. Sampling이 의미하는 것은 원본 이미지에 노이즈를 덮어씌어서 만든 xT에 대해서 다시 reverse markov process를 통해서 x0으로 만드는 과정을 수도코드로 나타낸 것이다.
(3) L_0
x1으로 부터 최종 x0을 복원하는 조건부 확률의 -log로 계산하였다. 일종의 Reconstruction Loss라고 볼 수 있다. 최종적으로 x1 → x0을 잘 구성하기 위한 재구성 손실이라는 것이다.
1.1 Data scaling, reverse process decoder, and L0
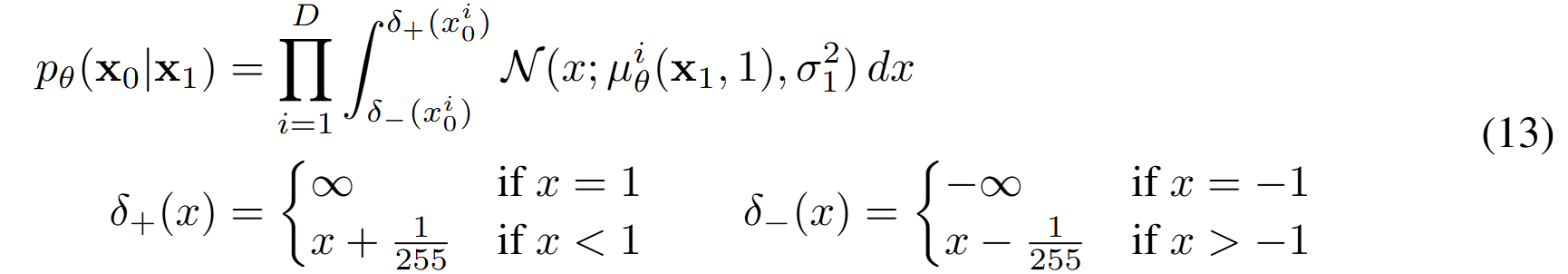
{0~255} image의 데이터 범위를 [-1, 1]로 스케일링한다고 한다. 이러한 처리가 신경망(revese process)가 표준 정규 prior p(xT)에서 시작하게 되어 스케일링 된 이미지로 갈 수 있도록 보장한다. Discrete한 log-likelihood를 얻기 위해, 저자는 reverse process의 마지막 항을 x1 가우시안 분포로부터 도출된 independent discrete decoder로 설정하였다.
마지막 단계(즉 x1→x0)에서, 연속 가우시안 N(x0;μθ(x1),σ^2I)를 ‘이산화’하여, 실제 픽셀 값([−1,1] 구간 중 특정 구간에 해당)으로 매핑하는 디코더를 정의한 것이다.
(13)항을 통해 도출되는 pθ(x0 | x1) 은 전이확률분포이자 이산적 확률분포이다. 즉, 확률질량함수(PMF)로써 모든 가능한 값에 대해 확률의 합이 1이 된다. 반면, 연속 확률 분포는 확률밀도함수(PDF)로 정의되며, 모든 실수 범위에 대해 적분하면 1이 된다. (13)항에서는 "구간 적분"을 수행함으로써, PMF를 얻은 것이다.
1.2 Simplified training objective


t는 [1, T] 범위에서 uniform하다. t = 1시점은 L0 항과 일치한다고 이야기한다. 무슨 말이냐면, L0이 의미하는 것은 마지막 단계 x1 → x0에서 x0을 복원할 때 드는 오차를 측정하는 것이므로 t = 1일 때, 해당 항이 L0의 근사라고 볼 수 있는 것이다. (13)항의 수식을 거쳐 이산 디코더를 사용해야하지만 실험적으로는 "가우시안 근사 x bin width"를 사용해 단순화했다.
1.3 Experiments


